基于非负矩阵分解的修正模糊聚类算法
李向利, 范学珍, 逯喜燕
(桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004)
聚类算法主要包括层次化聚类算法、 划分式聚类算法、 基于密度的聚类算法和基于网络的聚类算法[1-2]. 基于划分聚类算法的模糊聚类由于引入了模糊概念并扩展了硬聚类隶属度的取值范围[3-5], 有更好的聚类效果与数据表达能力, 因此已成为目前聚类分析中的研究热点[6-8].
由于传统的模糊C-均值[9](fuzzyC-means, FCM)算法存在对初始值敏感及收敛速度慢等缺点, 因此已提出了许多FCM改进算法. Hung等[10]通过对FCM算法的初始值进行细化, 提出了一种高效聚类的psFCM算法;
文献[11]提出了一种基于梯度的模糊C-均值(gradient-based fuzzyC-means, GBFCM)算法, 该算法利用梯度下降提高收敛速度和稳定性; 针对非常大的数据, Havens等[12]提出了LFCM和rseFCM算法, 通过核技巧的非线性聚类和放松收敛条件减少聚类复杂度; Krinidis 等[13]将局部空间信息和灰度信息以一种新的模糊方式相融合, 提出了模糊局部信息C-均值算法(fuzzy local informationC-means algorithm, FLICM); Zhou等[14]结合三角不等式, 提出了一种新的隶属度模糊C-均值聚类算法(new membership fuzzyC-means clustering algorithm, MSFCM), 减少了运算时间, 但该算法并不适用于高维度数据. 上述算法在解决复杂结构的高维度数据聚类问题时会出现大规模计算量导致聚类效果下降. 基于此, 本文提出一种基于非负矩阵分解(NMF)的修正模糊聚类(MFCM)算法(modified fuzzy clustering algorithm based on non-negative matrix factorization, MFCM-NMF), 该算法利用NMF进行降维, 并通过NMF提取数据的本质特征, 保留作为模糊聚类的聚类中心, 将NMF与MFCM相结合提出了新的目标函数, 并采用交替迭代算法进行求解, 且在迭代过程中基于三角不等式过滤出在下一次迭代中不改变其最近聚类中心的样本, 采用新的隶属度更新公式, 减少计算量, 提高聚类性能.
1.1 非负矩阵分解
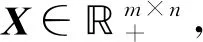
目前, 常用的重构误差构造主要使用欧氏距离和KL(Kullback-Leibler)散度.一般情况下, 采用基于欧氏距离的目标函数:
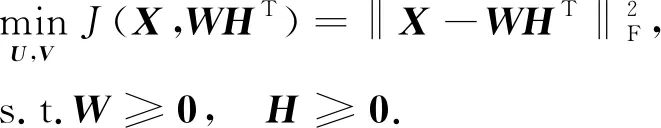
(1)
同时求解U和V时, 上述两种目标函数下的优化问题是非凸的, 但单独针对U或V求解时, 该问题即为凸的.采用乘性迭代规则可解决该问题并证明其收敛性, 通过固定U或V使用乘性迭代规则的方法交替更新, 其更新迭代公式为
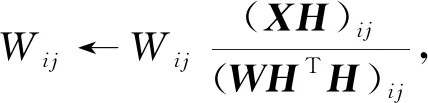
(2)
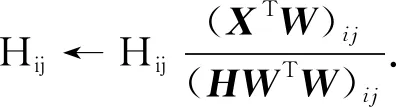
(3)
1.2 模糊C-均值聚类算法
模糊C-均值聚类算法[9]是一种基于划分的聚类算法, 其基本思想是使被划分到同一簇的对象之间相似度最大, 而不同簇之间的相似度最小. 模糊C-均值将n个样本xi(i=1,2,…,n)分到c个簇中, 每个簇的聚类中心为wi(i=1,2,…,c), 而uik∈[0,1]表示对象xk属于i类别的权重, 即可能性.利用隶属度将目标函数描述为如下形式:
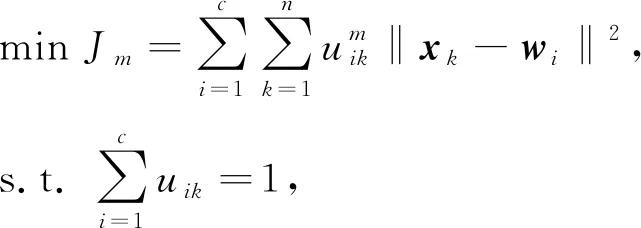
(4)
其中m为模糊加权指数.迭代公式为
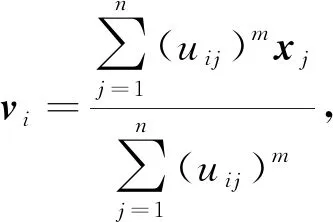
(5)
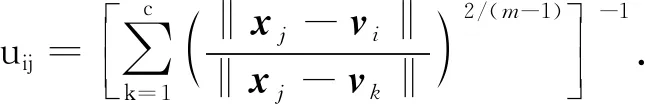
(6)
文献[14]在FCM的基础上引入了聚类中的三角不等式, 并给出了新的几何解释, 提出了一种新的隶属度缩放方法, 其基本思想是利用三角不等式过滤出在下一次迭代中不改变其最近聚类的样本, 根据一个放缩方案使簇内样本的联系增强, 簇外样本的联系减弱, 改进了传统FCM算法计算量大、 收敛慢等缺点.
2.1 目标函数
在较小矩阵上运行NMF算法可节省更多的时间和存储空间, 但也可能破坏数据样本间的本质结构, 影响聚类效果. 为减少负面影响, 本文希望在NMF压缩样本数据的过程中进行模糊聚类. 对于高维数据, 通过NMF提取样本的本质特征, 保留作为MFCM的聚类中心. 将NMF分解对原始数据样本的影响加入到FCM的目标函数中. 最小化代价函数为
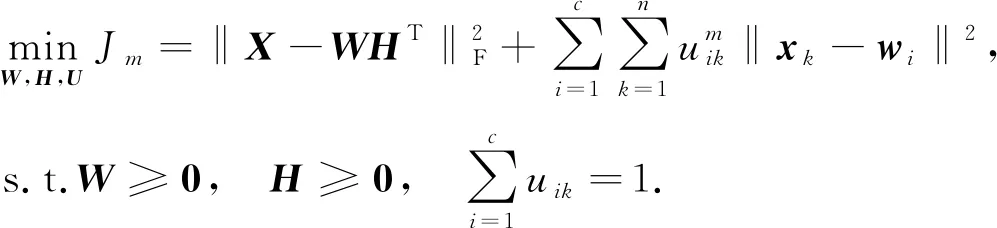
(7)
其中:m≥1;
xk为矩阵X的第k列;
uik∈[0,1]为隶属度矩阵U第i行、 第k列对应的元素, 表示第k个样本属于第i个簇的可能程度;wi为矩阵W的第i列.
2.2 目标函数优化求解
目标函数(7)中的第一项表示利用NMF算法处理原始数据的过程对聚类的影响程度, 第二项表示模糊C-均值对聚类的影响程度, 显然目标函数是非凸的, 求出其全局最优解不实际.因此, 利用交替迭代法则求解非凸函数的局部最优解, 通过迭代下列步骤解决优化问题, 直到收敛.
1) 若固定W和H, 通过uij最优化J, 则uij的更新准则为
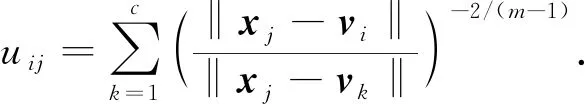
(8)
2) 若固定W和U, 通过H最优化J, 则H的更新准则为
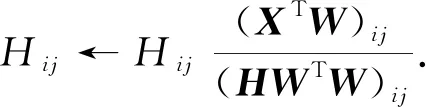
(9)
3) 若固定H和U, 通过W最优化J, 则可将目标函数(7)改写为
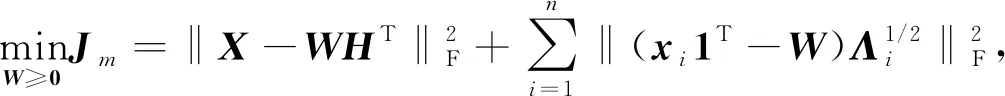
(10)
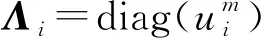
令φik为约束条件wik≥0的Lagrange乘子, 则目标函数(10)对应的Lagrange函数为
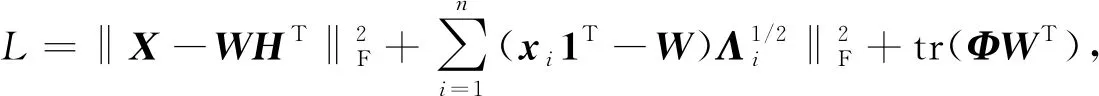
(11)
对W求偏导, 得
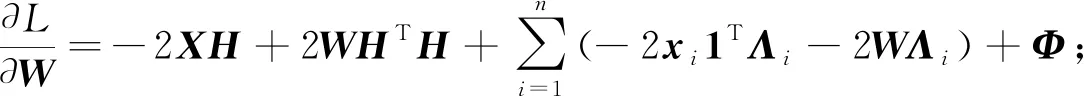
(12)
利用KKT(Karush-Kuhn-Tucker)条件φjkwjk=0(j=1,2,…,p,k=1,2,…,c), 可得
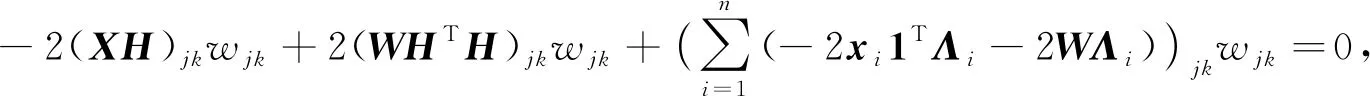
(13)
从而可得W的更新规则为
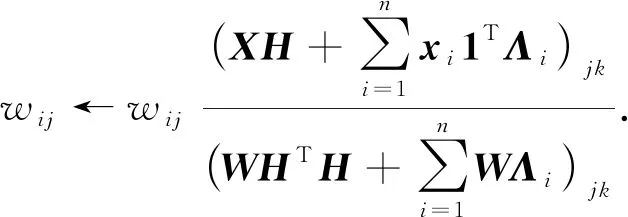
(14)
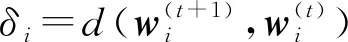
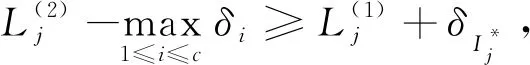
(15)
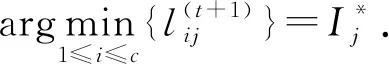
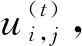
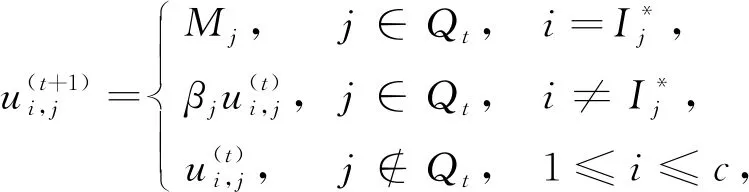
(16)
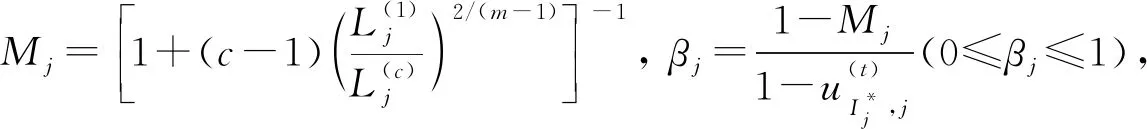
算法1MFCM-NMF算法.
输入: 原始非负矩阵X, 模糊系数m, 聚类个数c;
输出:U=U(t+1),V=V(t+1);
步骤1) 随机初始化U(0),W(0),H(0), 并根据式(14)计算出W(1), 令t=1;
步骤3) 利用式(8)计算U(t);
步骤4) 利用式(9)计算H(t);
步骤7) 根据式(15)过滤样本;
步骤8) 根据式(16)更新U(t+1);
步骤9) 根据式(16)更新H(t+1);
步骤10) 利用式(14)计算W(t+1);
步骤11) 若‖W(t+1)-W(t)‖≥ε, 则t=t+1, 返回步骤2), 否则停止.
本文不仅在数据集UCI上进行实验, 也在两个图像数据集和一个图片数据集上进行实验, 其中数据集UCI-satimage和UCI-wine来自于UCI机器学习数据库(https://archive.ics.uci.edu/ml/index.php). 本文选择几种经典的FCM算法作为对比算法:
传统FCM算法[9]、 LFCM算法[12]、 MSFCM算法[14]和MFCM-NMF算法, 在5个数据集上进行实验. 为避免初始值的影响, 每次实验FCM算法、 LFCM算法、 MSFCM算法和MFCM-NMF算法均采用相同的初始值, 且对比实验算法均取最优的模糊参数m值. 此外, 为避免随机性的影响, 每个实验均重复20次取平均值. 实验所用数据集的信息列于表1.

表1 数据集信息
为评估不同聚类算法的性能, 本文使用F-measure(F*)、 标准互信息(NMI)、 调整兰德指数(ARI)[17-18]3个外部指标进行聚类效果的评定, 这3个指标都是用于衡量真实分类与算法聚类结果的一致性, 其值越大聚类效果越好.
3.1 模糊参数的选择
模糊加权指数m是影响模糊聚类的重要参数[19-20]. 本文实验旨在说明聚类的性能波动受模糊加权指数m的影响. 在5个数据集上对MSFCM和MFCM-NMF算法进行对比实验, 结果如图1~图3所示. 其中: 参数m在[1.2,3.2]内的调节间隔为0.2, 带有相同颜色的虚线和实线是在同一数据集上分别利用MSFCM和MFCM-NMF算法获得的.
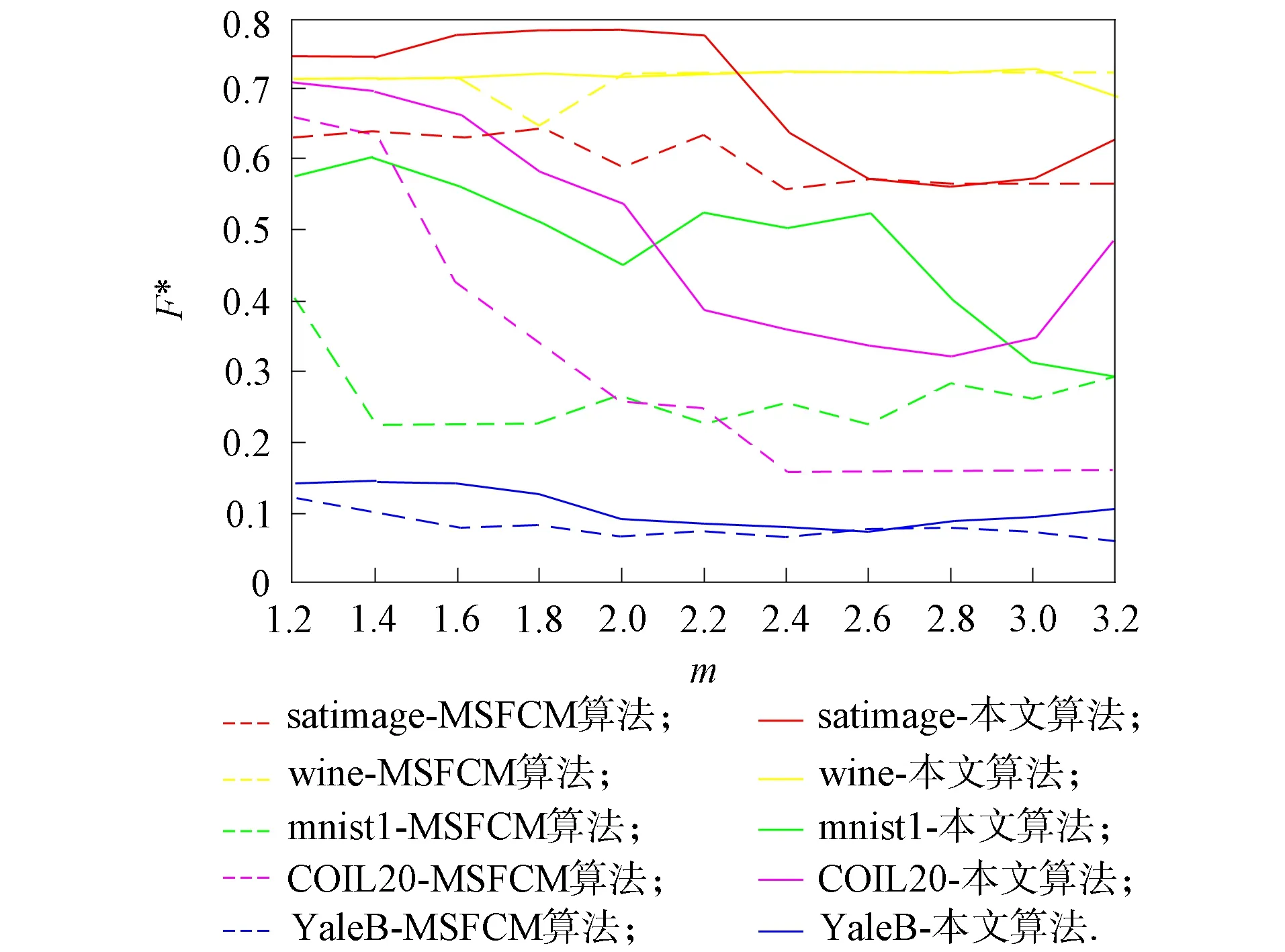
图1 F*随m的变化曲线
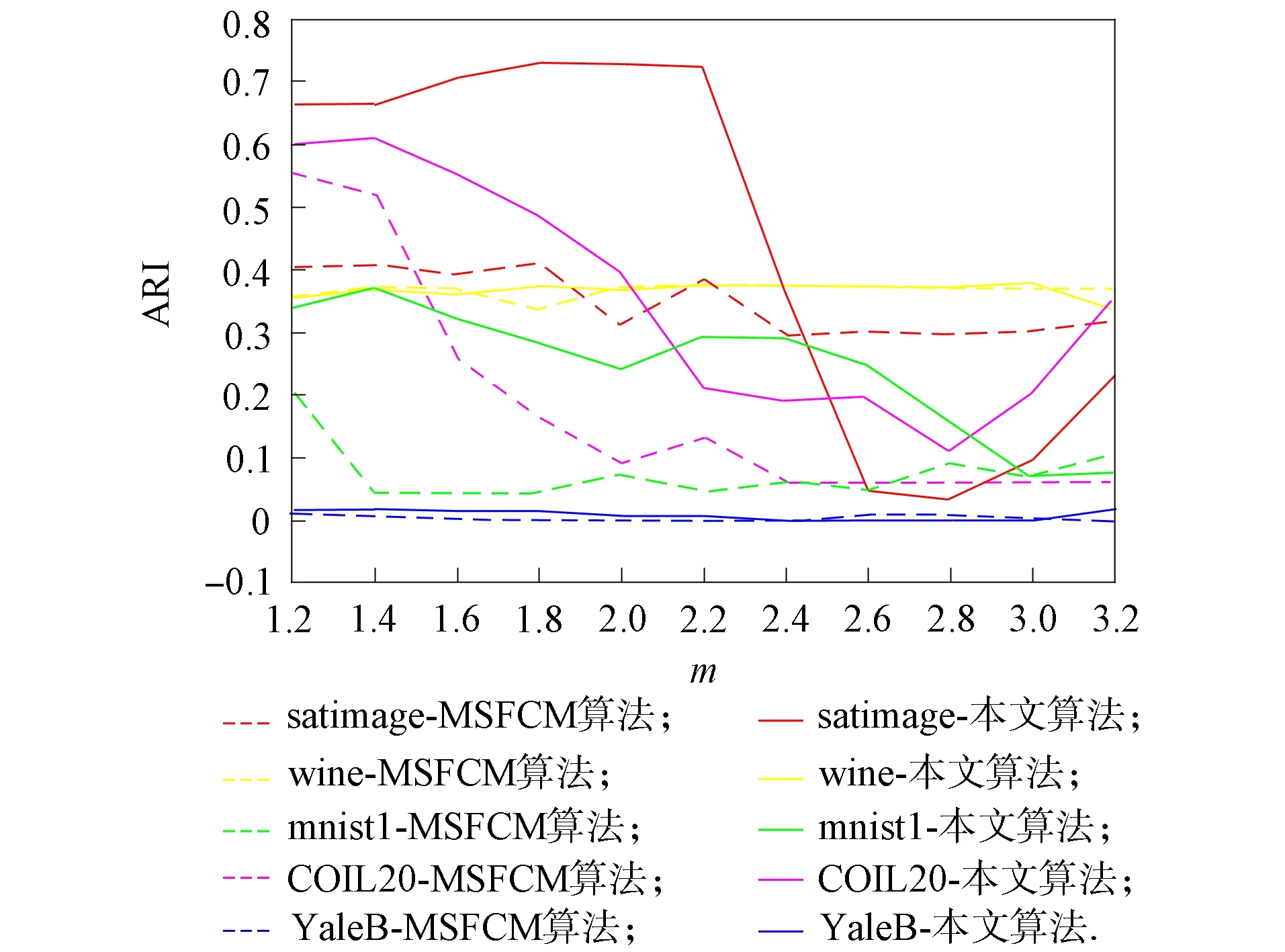
图2 ARI随m的变化曲线
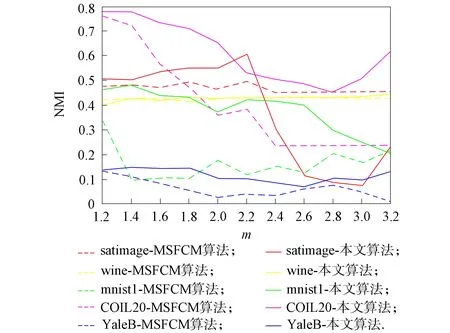
图3 NMI随m的变化曲线
由图1~图3可见:
1) MSFCM和MFCM-NMF算法的3个评价指标值均随m的改变而变动, 因此, 不同数据集所需的模糊指数m需要调整; 2) 图中的虚线为MSFCM算法得到的值, 实线为MFCM-NMF算法得到的值, 观察可见多数情况下实线位于虚线的上方, 表明MFCM-NMF算法优于MSFCM算法的聚类效果.
在数据集UCI-wine上, 由图1~图3可见, 黄色实线和虚线基本重合且基本无波动, 即在数据集UCI-wine上, 模糊参数m对MSFCM算法和MFCM-NMF算法的影响很小, 这主要是因为数据集UCI-wine的样本数少且维度低, 数据结构简单;
在数据集mnist1上, 易见表示MFCM-NMF算法的绿色实线始终位于表示MSFCM算法的绿色虚线上方, 即MFCM-NMF算法在3个评价指标上均优于MSFCM算法.
实验结果表明, 在结构简单的低维度数据集上, MFCM-NMF算法和MSFCM算法无明显区别, 但在高维度的复杂数据集上, 无论是数据集UCI还是图片数据集, MFCM-NMF算法均更优. 因此, 在数据集UCI-satimage上, 选择模糊参数m=2.2;
在数据集UCI-wine上, 选择模糊参数m=2;
在数据集mnist1上, 选择模糊参数m=1.4;
在数据集COIL-20上, 选择模糊参数m=1.2;
在数据集YaleB上, 选择模糊参数m=1.8.所有结果均为20次实验的平均值.
3.2 实验结果与分析
为直观地观察实验结果, 将最终的实验结果列于表2.由表2可见, 对于小样本数据集如UCI-wine, MFCM-NMF算法与MSFCM算法结果一致, 但在大样本数据集中, 例如在图片数据集COIL20中, MFCM-NMF算法在F*上相比于FCM,LFCM和MSFCM算法分别有0.217 7,0.217 7和0.202 6的提高, 在ARI上分别有0.219 3,0.219 3和0.207 6的提高, 在NMI上分别有0.251 9,0.251 9和0.171 9的提高. 在手写数字图片数据集mnist1的实验结果中, MFCM-NMF算法在F*上相比于FCM,LFCM和MSFCM算法分别有0.255 3,0.255 3和0.255 2的提高, 在ARI上分别有0.188 0,0.188 0和0.187 9的提高, 在NMI上分别有0.239 2,0.239 2和0.239 2的提高. 在较大维度数据集UCI-satimage的实验结果中, MFCM-NMF算法在F*上相比于FCM,LFCM和MSFCM算法分别有0.225 9,0.226 0和0.156 4的提高, 在ARI上分别有0.428 5,0.428 5和0.330 4的提高, 在NMI上分别有0.093 2,0.093 2和0.052 1的提高. 由实验结果可见, MFCM-NMF算法得到3个评价指标的值明显高于其他算法, 特别是在大维度的数据集上聚类效果评价指标有显著提高, 表明MFCM-NMF算法在大样本数据集上有明显优势, 可有效提高聚类效果.

表2 实验结果
3.3 过滤方案的效率
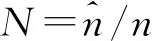
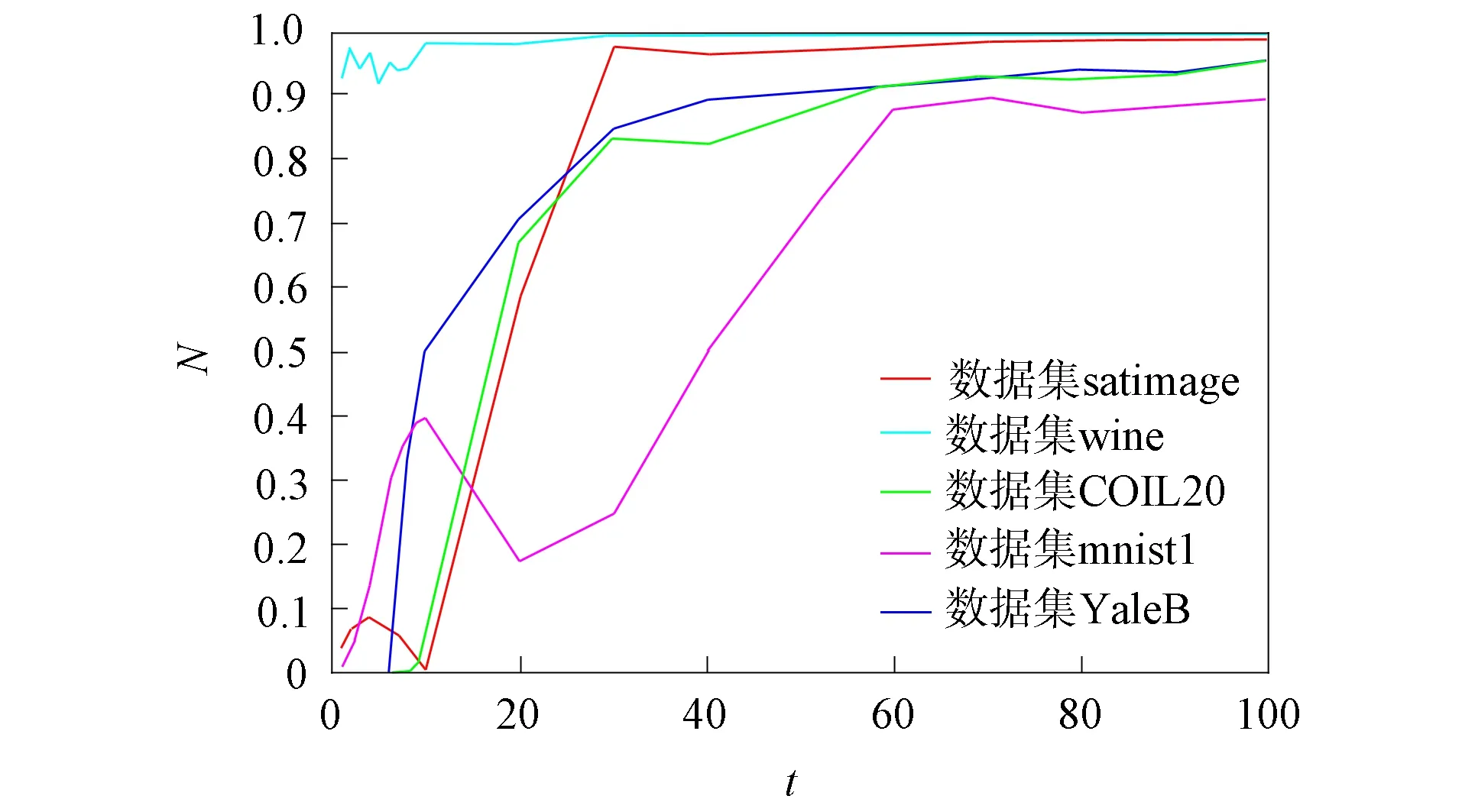
图4 N随迭代次数t的变化曲线
综上所述, 针对传统模糊聚类在解决复杂高维度数据集时出现大规模计算量导致聚类性能下降的问题, 本文将NMF与MFCM相融合, 提出了一种基于非负矩阵分解的修正模糊聚类算法(MFCM-NMF), 并用实验证明了该算法的有效性. 该算法将NMF的基矩阵与模糊聚类的聚类中心相结合, 提出了新的目标函数, 采用新算法进行交替迭代, 并采用新的隶属度更新公式, 对高维数据减少了计算量, 提高了聚类性能.
猜你喜欢集上聚类维度理解“第三次理论飞跃”的三个维度当代陕西(2022年4期)2022-04-19Cookie-Cutter集上的Gibbs测度数学年刊A辑(中文版)(2020年2期)2020-07-25链完备偏序集上广义向量均衡问题解映射的保序性数学物理学报(2019年6期)2020-01-13浅论诗中“史”识的四个维度中华诗词(2019年7期)2019-11-25基于K-means聚类的车-地无线通信场强研究铁道通信信号(2019年6期)2019-10-08分形集上的Ostrowski型不等式和Ostrowski-Grüss型不等式井冈山大学学报(自然科学版)(2019年4期)2019-09-09基于高斯混合聚类的阵列干涉SAR三维成像雷达学报(2017年6期)2017-03-26光的维度灯与照明(2016年4期)2016-06-05基于Spark平台的K-means聚类算法改进及并行化实现互联网天地(2016年1期)2016-05-04基于改进的遗传算法的模糊聚类算法智能系统学报(2015年4期)2015-12-27